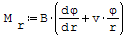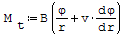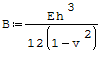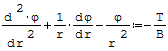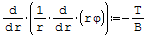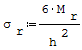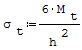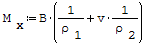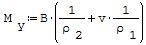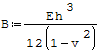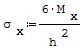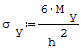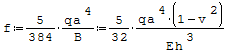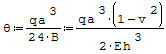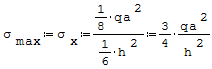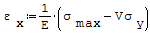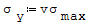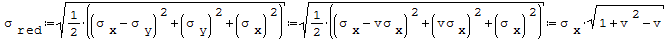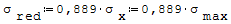Płyty

Poziomy elemnent konstrukcji, który oddziela poszczególne kondygnacje w budynku

Cienkie płyty kołowosymetryczne

Wzór na moment zginający w kierunku promieniowym:

Wzór na moment zginający w kierunku obwodowym:

gdzie:

- B- sztywność płytowa,

- v- liczba Poissona,

- r- promień,

- φ- kąt ugięcia,

- h- grubość płyty,

- E- moduł Younga.

Wzór na równanie różniczkowe środkowej powierzchni płyty kołowosymetrycznej:

gdzie:

- T- siła tnąca,

- B- sztywność płytowa,

- r- promień,

- φ- kąt ugięcia.

Wzór na maksymalne naprężenia od zginania:

gdzie:

- T- siła tnąca,

- r- promień,

- M_r- moment zginający w kierunku promieniowym,

- M_t- moment zginający w kierunku obwodowym,

- h- grubość płyty.

Zginanie ciękich płyt prostokątnych

Jeśli promień krzywizny warstwy obojętnej w oznaczymy przez ρ₁ dla płaczyzny xw, a ρ₂ dla płaszczyzny yw, to dla płyty odkształconej odpowiednie będą wzory na moment siły:

gdzie:

- B- sztywność płytowa,

- ρ₁- promień krzywizny warswy obojętnej w płaszczyźnie xw,

- ρ₂- promień krzywizny warswy obojętnej w płaszczyźnie yw,

- v- liczba Poissona,

- h- grubość płyty,

- E- moduł Younga.

Naprężenia przyjmują wartości maksymalne w przypowierzchniowych (skrajnych) włóknach płyt gdy płyta jest poddana czystemu zginaniu:

gdzie:

- M_x- moment gnący na osi x,

- M_y- moment gnący na osi y,

- h- grubość płyty.

Walcowe zginanie płyt

Wzór na maksymalne ugięcie w_max (strzałkę ugięcia):

gdzie:

- q- obciążenie ciągłe,

- a- szerokość,

- h- wysokość,

- v- liczba Poissona,

- B- sztywność płytowa,

- E- moduł Younga.

Wzór na kąt nachylenia stycznej na podporach:

gdzie:

- q- obciążenie ciągłe,

- a- szerokość,

- h- wysokość,

- v- liczba Poissona,

- B- sztywność płytowa,

- E- moduł Younga.

Naprężenia maksymalne od zginania w kierunku osi x, które występują w przypowierzchniowych (skrajnych) punktach płyty:

gdzie:

- q- obciążenie ciągłe,

- a- szerokość,

- h- wysokość.

Wzory na odkształcenia względne:

gdzie:

- v- liczba Poissona,

- E- moduł Younga,

- σ_max- naprężenia maksymalne od zginania w kierunku osi x, które występują w przypowierzchniowych (skrajnych) punktach płyty.

w wyniku tego otrzymujemy:

W przekroju w dolnych i górnych punktach o wspołrzędnej x=a/2 występują maksymalne naprężenia.

Wzór na maksymalne naprężenia według hipotezy Hubera:

gdzie:

- v- liczba Poissona,

- σ_x- maksymalne wartości naprężeń na osi x,

- σ_y- maksymalne wartości naprężeń na osi y.

Jeśli materiał ma liczbę Poissona v=0,3 (np.stal), wówczas naprężenia zredukowane wynoszą:

gdzie:

- σ_x- maksymalne wartości naprężeń na osi x,

- σ_max- naprężenia maksymalne od zginania w kierunku osi x, które występują w przypowierzchniowych (skrajnych) punktach płyty.