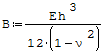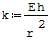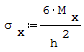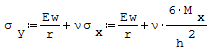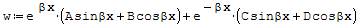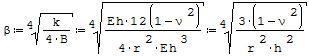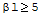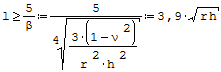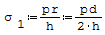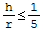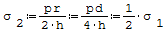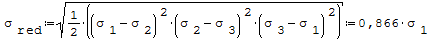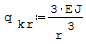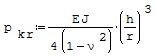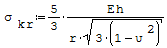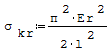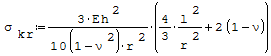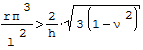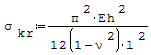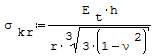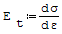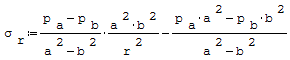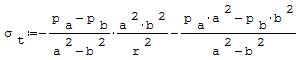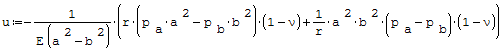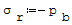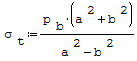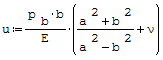Rura

Przewód, element konstrukcji o znacznej długości, najczęściej o przekroju kołowym używany np. do transportu gazów, cieczy.

Osiowosymetryczne zginanie rur cienkościennych

 

Wzór na sztywność zginania rury:

gdzie:

- ν- liczba Poissona,

- E- moduł Younga,

- h- grubość rury.

 

Wzór na stałą k oddziaływania podłoża sprężystego:

gdzie:

- E- moduł Younga,

- r- średni promień rury,

- h- grubość rury.

 

Wzór na maksymalne naprężenia pochodzące od zginania, które powstają w przypowierzchniowych powierzchniach rury, na kierunku wzdłużnym:

gdzie:

- M_x- moment gnący przypadający na 1 mm obwodu średniego w przekroju rury,

- h- grubość rury.

 

Wzór na maksymalne naprężenia pochodzące od zginania, które powstają w przypowierzchniowych powierzchniach rury, na kierunku obwodowym:

 

gdzie:

- M_x- moment gnący przypadający na 1 mm obwodu średniego w przekroju rury,

- h- grubość rury,

- σ_x- maksymalne naprężenia pochodzące od zginania, które powstają w przypowierzchniowych powierzchniach rury, na kierunku wzdłużnym,

- E- moduł Younga,

- r- średni promień rury,

- ν- liczba Poissona,

- w- ugięcie warstwy środkowej rury dla współrzędnej x.

 

Przemieszczenie dowolnego punktu w przekroju rury dla współrzędnej x:

gdzie:

- A- stała całkowania wyznaczona z warunków brzegowych,

- B- stała całkowania wyznaczona z warunków brzegowych,

- C- stała całkowania wyznaczona z warunków brzegowych,

- D- stała całkowania wyznaczona z warunków brzegowych,

- e- liczba Eulera,

gdzie:

- B- sztywność zginania rury,

- k- stała oddziaływania podłoża sprężystego,

- h- grubość rury,

- E- moduł Younga,

- ν- liczba Poissona,

- r- średni promień rury.

 

Gdy spełniony jest poniższy warunek:

rurę można traktować jako nieskończenie długą.

 

Uzyskujemy w ten sposób wzór:

gdzie:

- h- grubość rury,

- ν- liczba Poissona,

- r- średni promień rury,

- β- współczynnik.

 

Jeśli jest spełniony powyższy warunek, wówczas stałe całkowania A=B=0 we wzorze:

oraz wpływ brzegowych warunków na jednym brzegu na rozkład naprężeń i odkształceń na drugim brzegu rury jest pomijany.

 

Naprężenia w rurach cienkościennych lub powłokach walcowych poddanych działaniu ciśnienia wewnętrznego lub zewnętrznego

Wzór na naprężenia obwodowe:

gdzie:

- p- ciśnienie,

- r- średni promień rury,

- h- grubość rury,

- d- średnica.

 

Gdy:

wówczas naprężenia mają jednakową wartość na całej grubości rury.

 

Wzór na naprężenia wzdłużne, dla rury zamkniętej dnami, w obszar dostatecznie odległych od den:

gdzie:

- p- ciśnienie,

- r- średni promień rury,

- h- grubość rury,

- d- średnica.

 

Wzór na naprężenia zredukowane według hipotezy Hubera:

gdzie:

- σ₁- naprężenia obwodowe,

- σ₂- naprężenia wzdłużne,

- σ₃- naprężenie równe ciśnieniu p.

 

Wzór na krytyczną wartość obciążenia, w wyniku której dochodzi do wyboczenia:

gdzie:

- J- moment bezwładności przekroju poprzeczego pierścienia względem osi obojętnej przy zginaniu, która jest prostopadła do pierścienia,

- r- średni promień rury,

- E- moduł Younga.

 

Wzór na ciśnienie krytyczne, w wyniku którego kolista rura ulega wyboczeniu przejawiającemu się spłaszczeniem rury:

gdzie:

- J- moment bezwładności przekroju poprzeczego pierścienia względem osi obojętnej przy zginaniu, która jest prostopadła do pierścienia,

- r- średni promień rury,

- h- grubość rury,

- E- moduł Younga,

- ν- liczba Poissona.

 

Wyboczenie rur lub powłok walcowych poddanych równomiernemu ściskaniu osiowemu

1. Wzór na naprężenia krytyczne w ściskanej rurze przy wyboczeniu sprężystym (rura o dużej długości, mała grubość ścianki, rura ulega pofalowaniu):

gdzie:

- r- średni promień rury,

- h- grubość rury,

- E- moduł Younga,

- ν- liczba Poissona.

 

2. Wzór na naprężenia krytyczne w ściskanej rurze przy wyboczeniu (tak jak w przypadku pręta ściskanego osiowo), przekroje poprzeczne nadal mają kształt koła, na długości rury tworzt się półfala:

gdzie:

- r- średni promień rury,

- l- długość,

- E- moduł Younga.

 

3. Wzór na naprężenia krytyczne przy spłaszczeniu przekrojów poprzcznych, w których brzegi powłoki ściskanej osiowo mogą się swobodnie przemieszczać w kierunku radialnym:

gdzie:

- r- średni promień rury,

- E- moduł Younga,

- h- grubość rury,

- l- długość,

- ν- liczba Poissona.

 

4. Jeśli spełniony jest warunek dla krótkich walców cienkościennych:

gdzie:

- r- średni promień rury,

- h- grubość rury,

- l- długość,

- ν- liczba Poissona.

 

a powierzchnia walca ma tylko jedną półfalę, wówczas naprężenia krytyczne wyrażają się wzorem:

gdzie:

- r- średni promień rury,

- E- moduł Younga,

- h- grubość rury,

- l- długość,

- ν- liczba Poissona.

 

5. Wzór na naprężenia krytyczne, gdy obliczone naprężenia krytyczne są większe od granicy plastyczności, dla rur o znacznej grubości, są obecne odkształcenia plastyczne, a na rurze tworzą się osiowosymetryczne fale, które powstają przy naprężeniach krytycznych:

gdzie:

- E_t- moduł styczny, określony przez tangens kąta nachylenia stycznej do krzywej rozciągania,

- r- średni promień rury,

- h- grubość rury,

- l- długość,

- ν- liczba Poissona.

 

Obliczenie rur grubościennych

Wzór na napręrzenia promieniowe tzw. zadanie Lamego:

gdzie:

- p_a- ciśnienie zewnętrzne,

- p_b- ciśnienie wewnętrzne,

- r- promień,

- a- średnica zewnętrzna rury,

- b- średnica wewnętrzna rury.

 

Wzór na naprężenia obwodowe:

gdzie:

- p_a- ciśnienie zewnętrzne,

- p_b- ciśnienie wewnętrzne,

- r- promień,

- a- średnica zewnętrzna rury,

- b- średnica wewnętrzna rury.

 

Wzór na promieniowe przemieszczenie punktu rury:

gdzie:

- p_a- ciśnienie zewnętrzne,

- p_b- ciśnienie wewnętrzne,

- r- promień,

- E- moduł Younga,

- a- średnica zewnętrzna rury,

- b- średnica wewnętrzna rury,

- ν- liczba Poissona.

 

Wzór na największe naprężenia przy wewnętrznej powierzchni rury, jeśli działa tylko ciśnienie wewnętrzne p_b (tzn. p_a= 0):

gdzie:

- p_b- ciśnienie wewnętrzne,

- a- średnica zewnętrzna rury,

- b- średnica wewnętrzna rury,

- σ_t- naprężenie obwodowe,

- σ_r- naprężenie promieniowe.

 

Wzór na powiększenie się promienia wewnętrznego rury:

gdzie:

- p_b- ciśnienie wewnętrzne,

- a- średnica zewnętrzna rury,

- b- średnica wewnętrzna rury,

- E- moduł Younga,

- ν- liczba Poissona.