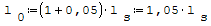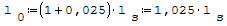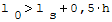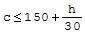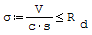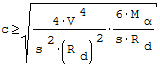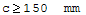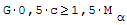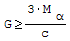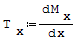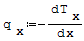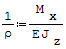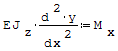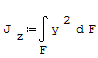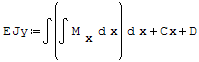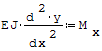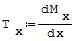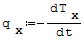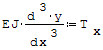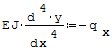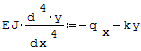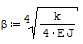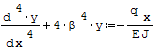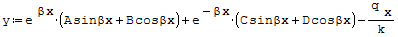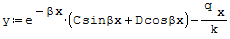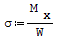Belka

Belka jest zginanym elementem konstrukcji.

 

Prostoliniowe elementy prętowe, przenoszące najczęściej na podpory prostopadle działające obciążenia do osi belek (m. in. elementy nośne stropów, pomostów, konstrukcji wsporczych, nadproży, wsporników).

 

Belki pełnościenne- wykonane z kształtowników walcowanych na gorąco, profilowanych na zimno lub z blach. Wyróżniamy belki: pojedyncze (stropowe, pomostowe), złożone (skrzynkowe) oraz dwugałęziowe (podciągi stropowe).

 

Belki ażurowe- środnik w nich jest podwyższony i ma otwory zmniejszające ciężar belki i umożliwiające przeprowadzenie przewodów. Dzięki podwyższeniu przekroju belki można zwiększyć nośność i sztywność belki w stosunku do kształtownika z którego jest wykonany.

 

Belki kratowe- lekkie elementy stropów i dachów, dżwigary o dużych rozpiętościach i obciążeniach, znajdujące zastosowanie w mostach, suwnicach, ekskakadach.

 

Belki jednoprzęsłowe- swobodnie podparte na końcach lub utwierdzone. Mogą być swobodnie podparte jednoprzęsłowe lub ze wspornikami. Belki wspornikowe i obustronnie utwierdzone są rzadko stosowane ponieważ należy je odpowiednio umocować w ścianach.

 

Belki wieloprzęsłowe- trudno wykonać ich połączenia z innymi belkami. Są wrażliwe na zmiany temperatury i osiadanie. Ich wykonanie wymaga zużycia mniejszej ilości stali niż dla belek jednoprzęsłowych.

Rozpiętość obliczeniowa belki l_o- odległość między teoretycznymi punktami podparcia. Gdy belka jest podparta na łożyskach, to odległość l_o równa jest odległości między ich osiami.

Wzory dla belek:

 

a) jednoprzęsłowych swobodnie podpartych lub obustronnie utwierdzonych:

gdzie:

- l_s- odległość w świetle między ścianami lub łożyskami.

 

b) skrajnych przęseł belek ciągłych oraz belek jednoprzęsłowych jednostronnie utwierdzonych:

gdzie:

- l_s- odległość w świetle między ścianami lub łożyskami,

- h- wysokość belki.

 

Długość zamocowania belek utwierdzonych

Dla ściany betonowej lub ceglanej określa się z warunku na docisk belki do ściany równomierne oparcie belki walcowanej o długości do 6 m:

gdzie:

- c- długość oparcia [mm],

- h- wysokość belki [mm].

 

Nacisk wywierany na powierzchnię podparcia:

gdzie:

- V- obliczona wartość reakcji belki,

- s- szerokość półki (stopki),

- R_d- wytrzymałość na docisk obliczona dla muru lub betonu.

 

Długość zamocowania belek utwierdzonych (warunek docisku belki do ściany):

gdzie:

- M_α- moment utwierdzenia belkli w ścianie przy uwzględnieniu obliczonych wartości obciążeń,

- V- obliczona wartość reakcji belki,

- s- szerokość półki (stopki),

- R_d- wytrzymałość na docisk obliczona dla muru lub betonu.

 

Obliczeniowy ciężar ściany G, który jest powyżej wspornika:

gdzie:

- c- długość oparcia [mm],

- M_α- moment utwierdzenia belkli w ścianie przy uwzględnieniu obliczonych wartości obciążeń.

 

Belka zginana

 

Zgodnie z warunkami równowagi pewnego rozpatrywanego odcinka belki siła tnąca jest równa pochodnej monetu gnącego:

gdzie:

- M_x- moment gnący,

- x- długość belki.

 

Pochodnej siły tnącej o przeciwnym znaku (ponieważ wygina się przeciwnie do wskazówek zegara) i jest równe obciążenie ciągłe:

gdzie:

- T_x- siła tnąca,

- x- długość belki.

Wzór na promień krzywizny belki:

gdzie:

- M_x- moment gnący,

- E- moduł Younga,

- J- moment bezwładności.

 

Porównując powyższy wzór ze wzorem na promień krzywizny linii, otrzymamy równanie różniczkowe dla linii ugięcia zginanej belki:

 

Wzór na moment bezwładności przekroju:

gdzie:

- y- współrzędna,

- F- pole przekroju,

- E- moduł Younga,

- J- moment bezwładności.

 

Wzór na równanie linii ugięcia belki:

Z warunków brzegowych wyznacza się stałe całkowania C i D.

 

Belka na sprężystym podłożu

 

Ze wzorów:

gdzie:

- E- moduł Younga,

- J- moment bezwładności,

- M_x- moment gnący,

- T_x- siła tnąca,

- q_x- obciążenie ciągłe.

 

Wynikają wzory:

gdzie:

- E- moduł Younga,

- J- moment bezwładności,

- M_x- moment gnący,

- T_x- siła tnąca,

- q_x- obciążenie ciągłe.

 

Na belkę leżca na sprężystym podłożu działa obciążenie ciągłe oraz reakcja podłoża (teoria Winklera).

 

Wzór ma postać:

gdzie:

- EJ- sztywność zginania belki,

- E- moduł Younga,

- J- moment bezwładności,

- q_x- obciążenie ciągłe na 1 mm długości belki (N/mm),

- k- stała sprężysta podłoża (N/mm²).

 

Wprowadzamy oznaczenie:

gdzie:

- E- moduł Younga,

- J- moment bezwładności,

- k- stała sprężysta podłoża (N/mm²).

 

Wzór ma postać:

gdzie:

- EJ- sztywność zginania belki,

- E- moduł Younga,

- J- moment bezwładności,

- q_x- obciążenie ciągłe na 1 mm długości belki (N/mm),

- k- stała sprężysta podłoża (N/mm²).

 

Rozwiązanie równania:

A, B, C, D to stałe całkowania wyznaczone z warunków brzegowych.

 

Gdy βl≥5 (belki długie) stałe A i B równe są zeru i równanie linii ugięcia belki leżacej na sprężystym podłożu ma wzór:

gdzie:

- q_x- obciążenie ciągłe na 1 mm długości belki (N/mm),

- k- stała sprężysta podłoża (N/mm²).

 

Wzór na maksymalne naprężenie:

gdzie:

- M_x- moment gnący.